Forecast-Free Algorithms: A New Benchmark For Tactical Strategies

We all spend most of our time creating strategies with the promise of “alpha”—excess returns adjusted for risk to some benchmark. The most desirable strategies for many traders/investors are tactical asset allocation models because they are easy to implement and tend to be more reliable than capitalizing on short-term effects that are constantly in flux. One of the “founding fathers” of tactical asset allocation was Mebane Faber http://www.mebanefaber.com/2009/02/19/a-quantitative-approach-to-tactical-asset-allocation-updated/. He showed the utility of using long-term moving averages to trade various asset classes. This simple approach worked very well both in and out of sample, and also managed to preserve capital. Some of his other papers validated other academic work showing the utility of momentum/relative strength to choose between asset classes as well. Jeff Pietsch of ETF Prophet http://etfprophet.com/ has written about several different types of relative strength models for broad asset classes—many of them worth reading. There are also some basic models offered to follow on the site.  Michael Stokes at MarketSci http://marketsci.wordpress.com/ also has published  research and has a monthly model for investors to follow. All of the models above use return or price inputs in order to predict 1) whether an asset is likely to have a positive or negative return and 2) which assets will perform the best in the future.  In a sense, both models are dependent on forecasting either absolute or relative  returns and/or prices. If the past doesn’t predict the future, then such models fail to produce alpha.

But what should be the benchmark for such strategies? I would argue that a fair benchmark would be a model that is “forecast-free”– in the sense that it does not extrapolate returns or prices. Such a model would be also risk neutral and seek to maximize diversification. In the absence of opinions about relative returns, we would seek to treat each asset class equally and reduce the dependency or correlation between them. This portfolio would be agnostic to relative returns, and theoretically should be optimal if the market was truly efficient. As it turns out, such a portfolio does a lot better than you might expect—-implying that 1) assets are much more efficiently priced than we think 2) tactical asset allocation models offer varying “beta” payoffs– a) they either reduce downside risk (unfavorable beta) while preserving the upside (favorable beta) similar to trend-following models using moving averages and cash holdings –for a good overview of the literature read Automated Trading Systems http://www.automated-trading-system.com/ , or  b) they create beta through relative asset selection— dynamically increasing leverage in up markets by selecting the most volatile assets, and subsequently reduce leverage by selecting the least volatile assets in down markets.

I have conducted exhaustive testing on such a “forecast-free” model  and related variants that I like to term the “Minimum Correlation Algorithm.” It is perhaps the most robust model or “system” that I have ever tested– in the sense that it is largely invariant to the selection of assets or parameter values and furthermore it performs very well on a risk-adjusted basis. Below is a simple test using 8 major asset classes/indices including: 1) S&P500 2) Nasdaq 100 3) Russell 2000 4) MSCI EAFE (Europe, Asia and Far-East) 5) Long-term Treasury Bonds 6) Real Estate and 7) Gold.  Note that rebalancing was done on a weekly basis and quarterly data was used within the algorithm to estimate correlations.

 

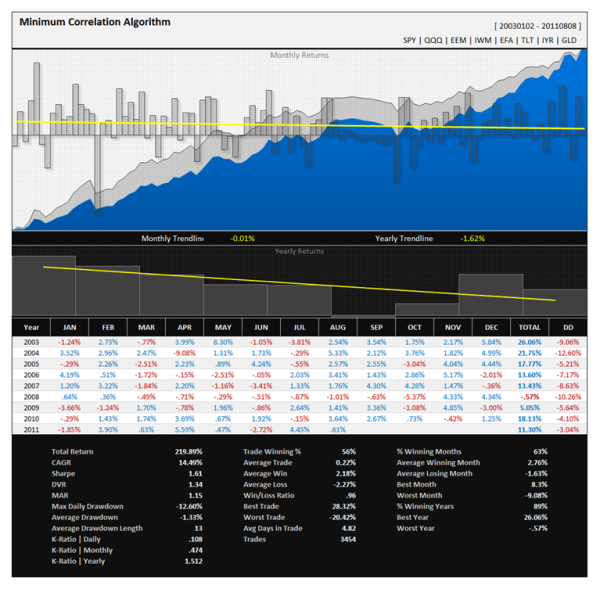Looks pretty good doesn’t it? Notice that this method often performs very well in difficult times (like this month!). It is hard to believe that this strategy is always invested in the market and does not care whether assets are going up or down. Considering this is not a “system” of any sort, nor does it rely on parameters or multiple assumptions about market inefficiencies, it is truly an impressive result. It turns out that Markowitz was right– diversification is where it is at. Consider these results all the more impressive as correlations between assets have been increasing since 2000.  To me this is the true benchmark for a tactical asset allocation strategy– the sharpe ratio of such a strategy should exceed that of the “forecast-free” approach in order to justify the risk, not to mention the fact that such strategies rely substantially on specific parameters that are constantly in flux (ie 10-month sma or 12 month roc).

I am not advocating against active management or tactical asset allocation. In fact I believe there are ways to dramatically improve upon such models using heuristic portfolio algorithms. This is a topic I will cover at some point in the future- perhaps in a white paper.  I am merely suggesting that the backtests of tactical models are not quite as impressive in light of the fact that you can probably do better looking both at in-sample and out-of-sample by sticking with a more robust approach of just diversifying intelligently. There are many further applications of this approach– one of the most obvious is to diversify among different trading systems or investment managers. A less obvious application would be to use the algorithm to create  “learning ensembles” that blend different system signals into one composite voting mechanism or trading signal.